V-T-diagram

Syfte:

Syftet är att undersöka kopplingen mellan s-t-diagram (läge-tid-diagram) och v-t-diagram ( hastighet-tid.diagram). Samt undersöka olika samband mellan dessa diagram.

Mål:

·         Registrera en vagns rörelse i synkroniserade s-t-diagram och v-t-diagram.

·         Avläsa ur och förklara sambandet mellan värden i s-t- repsekttive v-t- diagrammet och bestämma hur dessa i sin tur hänger ihop med vagnens verkliga rörelse.

·         Bestämma och tolka arean under v-t-grafen.

Material:

Under undersökningen användes dator med PASCO capstone program, vagn, med vagnbana (2 m), rörelsesensor, ett usb pasport mellan sensorn och datorn.

Utförande:

Vi ställde upp banan på en overhead för att få en lutning så att vi kunde få en acceleration på vägen ner (se tidigare inlägg andragradsfunktionen). Sensorn ställde vi i ”början” på banan (den delen som är i botten). Sedan puttades vagnen upp för banan samtidigt som pasco programmet och sensorn fångade upp vagnens rörelse och överförde detta i ett diagram samtidigt som hela rörelsen filmades.

Resultat:

I tabellerna nedan kan vi avläsa, tiden (s), läget (m) och hastigheten (m/s). Alla dessa är synkroniserade så att vid tex vid mätvärde 41 hade det gått 2,000 sekunder (s), vagnen var då 1.83 meter ifrån sensorn och hade en hastighet på 0,27 m/s. Vid ett mätvärde 51 hade vi en negativ hastighet, -0,46 m/s, positionen var 1,77 meter ifrån sensorn och det hade gått 2.500 sekunder sedan mätningarna startade. Om vi jämför 41 0ch 51 kan vi se att vagnen var närmare sensorn i 51 trots att det hade gått längre tid, detta indikerar att vagnen är på väg tillbaka mot sensorn. Hastigheten blir negativ eftersom att vagnen rör sig mot den förutbestämda positiva riktningen som är från sensorn, när vagnen rör sig mot sensorn   rör det sig i negativ riktning och  hastigheten blir likaså negativ.

Vändpunkten hittar vi lätt i tabellen, det är det ställe så hastigheten är negativ och där avståndet från sensorn minskar. När vagnen vänder står den still i några delar var en sekund. Vi kan se att från 2,100 sekunder till 2.250 sekunder befinner sig vagnen hela tiden på 1.85 meter ifrån sensorn.  Samtidigt minskar hastigheten hela tiden ovh vid det mittersta värdet står det still, 0,03 m/s.

Tabellerna visar en vagns rörelse i tid, läge och hastighet.

För att få reda på hur långt vagnen färdades  beräknar man arean under v-t-grafen.

På bilden ser vi v-t-grafen under det första tidsintervallet, innan den har nått vändpunkten. Arean under grafen är markerad, arean under får vi som förflyttningen.

Av PASCO capstone får vi att arean under grafen är 1.33 m/s*s. Detta medför att förflyttningen 1.33 m.

m/s*s= (m*s)/s= (m*s)/s = m/1 = m

Först flyttar vi upp s och multiplicerar den med m, genom att s står ovanför bråkstrecket blir det lättare att se att vi kan stryka s mot s, detta visas steg 3. När vi stryker ett tal finns alltid 1 kvar. Detta betyder att vi delar m på 1 vilket är samma sak som m.

1,33 m/s*s = 1.33 m’

Beviset ovan styrker att vi kan för korta m/s*s till m.

På bilden ser vi samma förflyttning som på bilden ovan, men här ser vi även s-t-diagramet.

Vi kan se att vi får samma värden i de båda graferna.

I den blåa får i ta Δ s (”delta s”), det betyder att vi subtraherar läge 2 från läge 1.

S₁ = 0.850 s och 0.52m

S₂= 2,200 s och 1,85 m

Δs = 1,85- 0,52 = 1.33 m.

Vi fick samma resultat av att beräkna Δs och att ta arean under v-t-grafen.

I uträkningen ovan ser vi att det går att stryka s mot s i enheten och att vi får m kvar ensamt, m står för läget.  Detta ger oss att vagnen färdades 1.33 m innan de vände och åkte neråt.

Vi kan beräkna förflyttning på vägen tillbaka på samma sätt, men då får vi arean mellan x-axeln och grafen.

På bilden ser vi förflyttningen för vagnen efter vändpunkten.

-1.55 m/s*s = -1.55 m 

På bilden ser vi arean under v-t.grafen synkad med s-t-diagram.

Vi kan se att vi får samma värden i de båda graferna.

I den blåa får i ta Δ s (”delta s”), det betyder att vi subtraherar läge 2 från läge 1.

S₁ = 2.150s och 1,85m

S₂= 3.650 s och 0.30 m

Δs = 0.30- 1,85 =-1.55m.

Vi fick samma resultat av att beräkna Δs och att ta arean under v-t-grafen.

Av beviset ovan vet i att arean under grafen är förflyttningen. Att vi har en större förflyttning efter vändpunkten än innan kan bero på att vi stannade vagnen närmare sensorn är vad vi startade den.

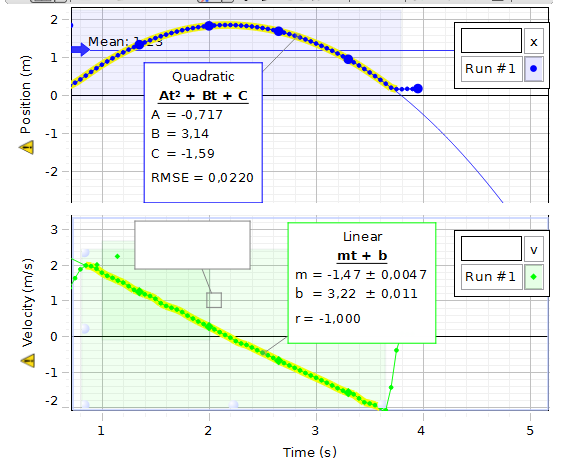
På bilden ser vi de båda graferna med sina ekvationer.

I koordinatsystemen ovan visas grafen för vagnen rörelse, blå graf, och grafen för vagnens hastighet, den gröna. 

Nollpunkter 3.68 och 0.51. Nollpunkterna visar när vagnen är bredvid sensorn. Eftersom att vi startade vagnen framför och stannade vagnen framför, är dessa värden inte kopplade till verkligheten. Likaså alla värden bakom nollpunkterna, de är bara matematikens beskrivning av hur verkligheten skulle ha sett ut om vi lät vagnen fortsätta i all evighet. Detta skulle inte fungera eftersom att den energin vi puttade på bilen med inte är med som en faktor i matematikens värld. Energin hade inte räckt till att putta upp vagnen för en oändlig backe. Här har matematiken en begränsning, den tar inte hänsyn till alla faktorer i verkligheten som spelar in när man gör en mätning som denna.